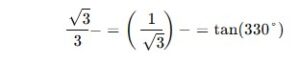القيمة الدقيقة للدالة المثلثية t a n 330 ° مستخدماً الزوايا المرجعية تساوي

إجابة سؤال: القيمة الدقيقة للدالة المثلثية t a n 330 ° مستخدماً الزوايا المرجعية تساوي

الجواب: القيمة الدقيقة للدالة المثلثية t a n 330 ° هي – 1/√3 أو – (3√/3).

شرح الإجابة:

لحساب القيمة الدقيقة للدالة المثلثية tan(330°)، نبدأ أولاً بتحديد موقع الزاوية في الدائرة المثلثية. الزاوية 330° تقع في الربع الرابع من الدائرة المثلثية. بالنسبة للزوايا في هذا الربع، فإن الدوال المثلثية التانجينت تكون سلبية لأن الجيب موجب ولكن الجتا سالب.

الخطوة التالية هي استخدام الزاوية المرجعية 30°، وهي الزاوية التي تبعد عن 330° بمقدار 360° – 330° = 30°. إذن، نعتبر الزاوية المرجعية 30° في حساباتنا.

نعلم أن tan(30°) = 1/√3، وهذه القيمة هي التانجينت للزاوية 30° في الربع الأول.

نظرًا لأن tan(θ) في الربع الرابع يكون سالبًا، فإن tan(330°) تساوي -tan(30°)، أي: